Производная от натурального числа е

Тогда получим:. Если в каждой точке промежутка существует производная, то говорят, что функция дифференцируема на этом промежутке. Правила вычисления производных.

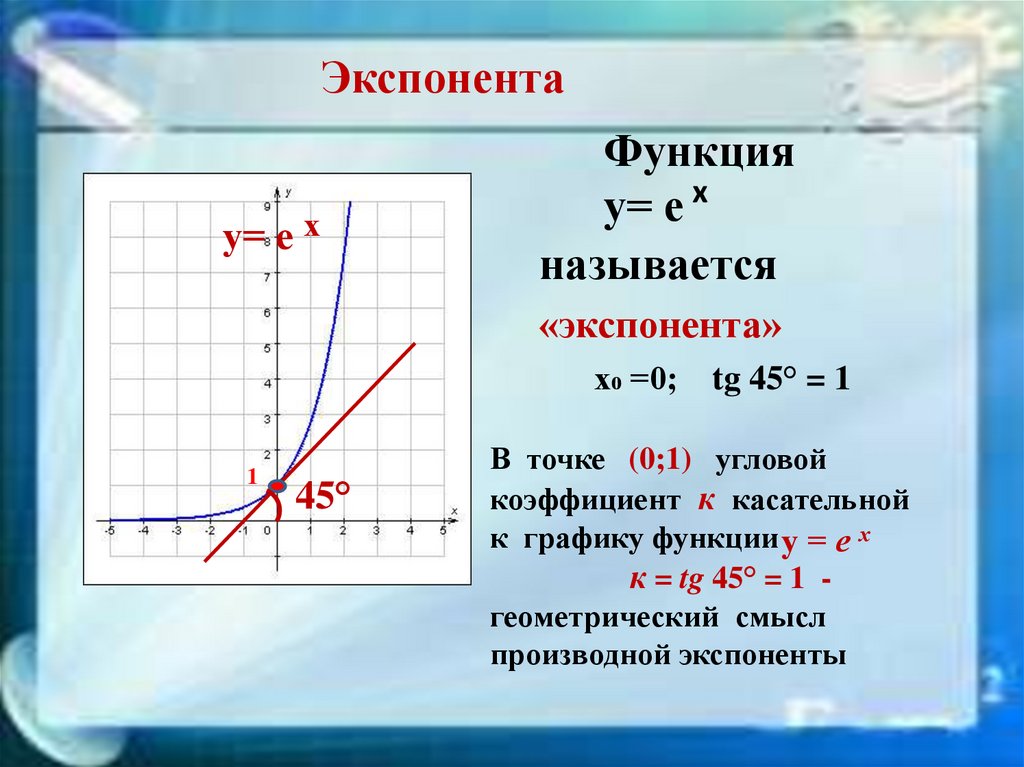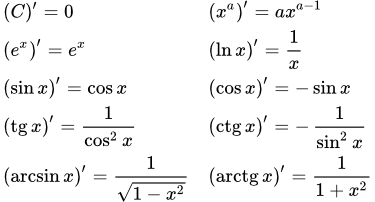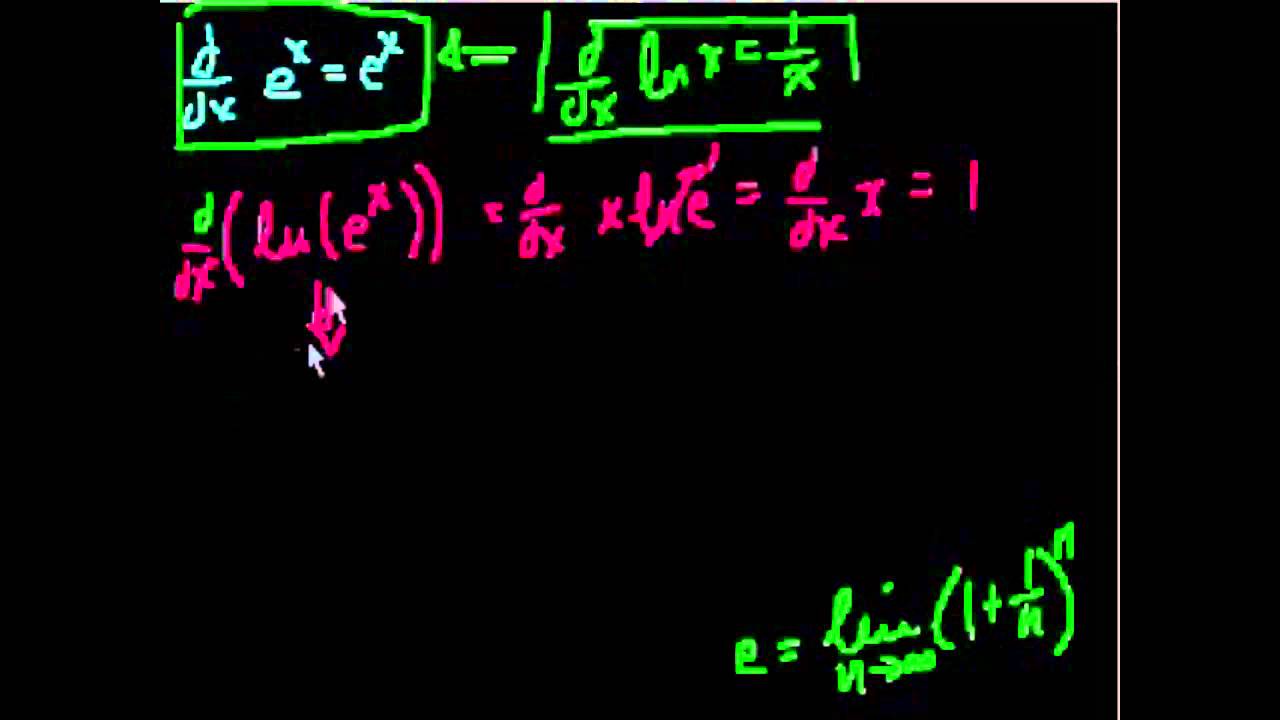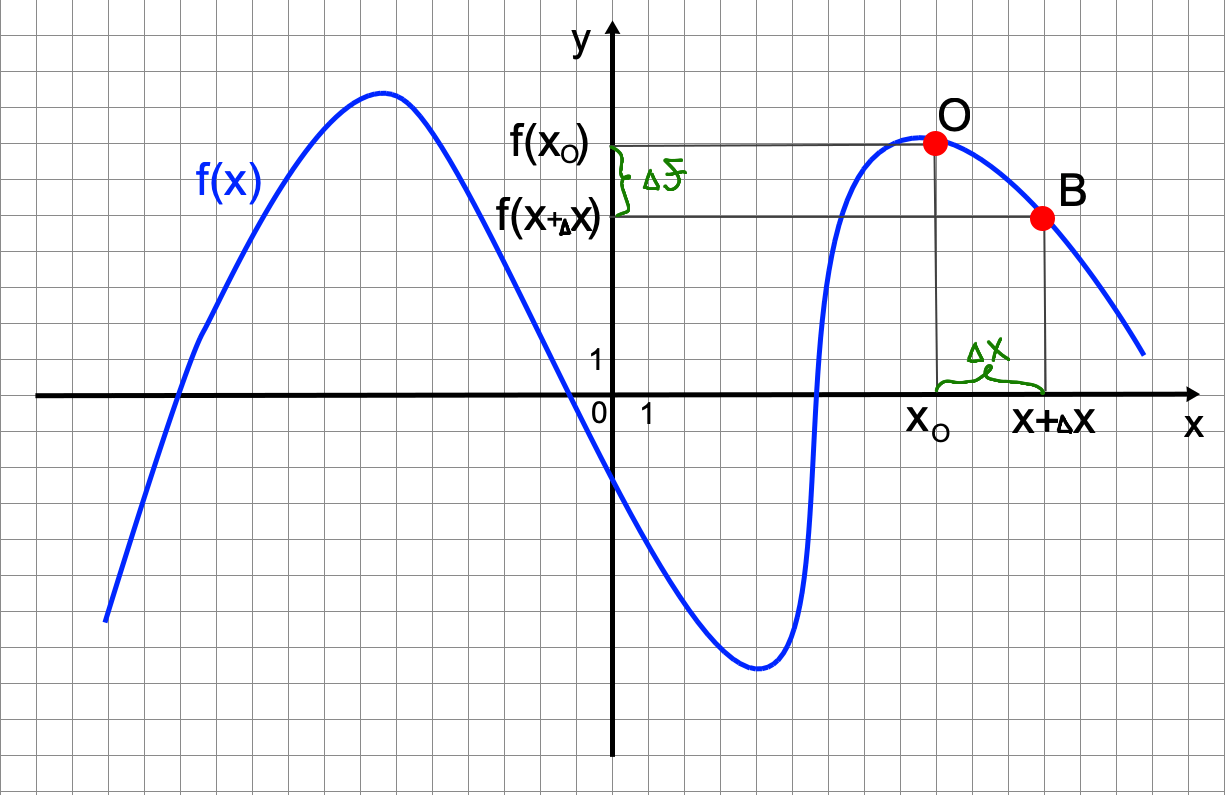
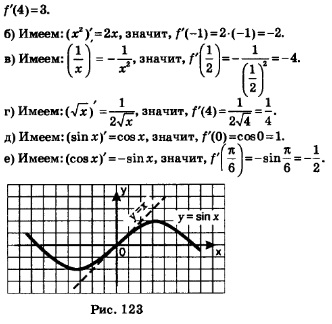
Таблица производных

Эта непрерывная дробь не периодическая. Записана в линейной нотации. Первые знаков после запятой числа e [ 1 ]. Приблизительно равно 2, Обозначается строчной латинской буквой « e ».

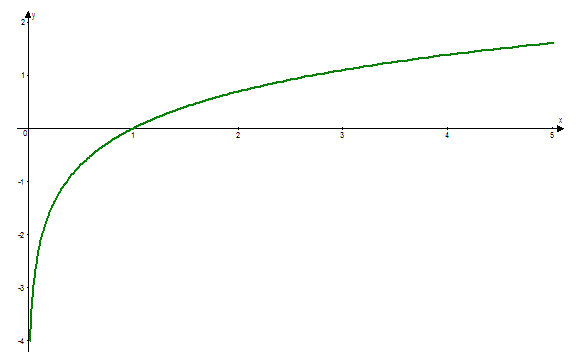
Как и экспонента, логарифмическая функция относится к категории трансцендентных функций. Натуральные логарифмы полезны для решения алгебраических уравнений , в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. В приложениях натуральный логарифм участвует в математическом описании таких процессов, в которых скорость изменения некоторого количества в каждый момент обратно пропорциональна самому количеству. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества : чем больше атомов распадается, тем меньше их становится и тем медленнее идёт дальнейший процесс.

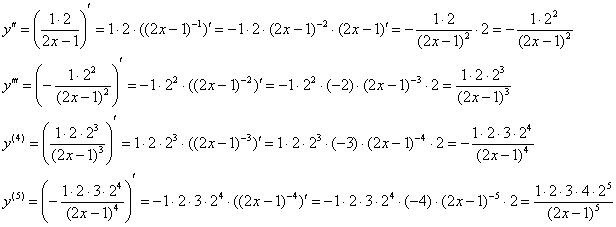
Элементарными функциями считаются и те функции, которые могут быть получены из основных элементарных функций с помощью конечного числа арифметических действий и композиций. Формулы, позволяющие находить производные основных элементарных функций, называются формулами дифференцирования. Напомним формулы вычисления производных некоторых элементарных функций:. В этой статье рассмотрим формулы дифференцирования других элементарных функций. Разумеется, если этот предел существует и конечен.

Похожие статьи

• Бусы из натуральных камней синего цвета
• Смотреть порно большие сиськи натуральные без силикона
• Архитектурное бюро из натурального ка
• Порно натуральных сисек в жопу